Hiệu ứng

Menu

Blogroll

"Nếu không thử vì sợ thất bại thì bạn không hề tôn trọng tuổi trẻ và thời gian của mình...... Nếu cô ta tuyệt vời, cô ta sẽ không dễ dàng. Nếu cô ta dễ dàng, cô ta sẽ không tuyệt vời. Nếu cô ta xứng đáng, bạn sẽ không bỏ cuộc. Nếu bạn bỏ cuộc, bạn không xứng đáng... Sự thật là, tất cả mọi người sẽ làm bạn tổn thương; điều quan trọng là bạn tìm ra được người đáng cho bạn chịu đựng khổ đau..... Nếu có một cô gái sẵn sàng chết vì bạn,bạn biết vì sao không, nó chứng tỏ cô ấy thà chết còn hơn phải yêu bạn.

Tìm kiếm

Thứ Năm, 22 tháng 5, 2014

Inequality 5: Chứng minh rằng $\sum \dfrac{a}{a^2-bc+1} \geq \dfrac{1}{\sum a}$

Bài toán (Macedonia National Olympiad 2009)
Cho các số thực dương 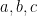a,b,c thoả mãn ab+bc+ca=\dfrac{1}{3}. Chứng minh rằng :
\dfrac{a}{a^2-bc+1}+\dfrac{b}{b^2-ca+1}+\dfrac{c}{c^2-ab+1}\geq \dfrac{1}{a+b+c}
Lời giải :
Sử dụng BĐT Cauchy-Schwarz, ta được :
\left ( \underset{sym}{\sum}\dfrac{a}{a^2-bc+1} \right )\left ( \underset{sym}{\sum}a(a^2-bc+1) \right )\geq \left ( a+b+c \right )^2
Kết quả này tương đương :
\underset{sym}{\sum}\dfrac{a}{a^2-bc+1}\geq \dfrac{(a+b+c)^2}{a^3+b^3+c^3+a+b+c-3abc}
Do vậy việc chứng minh kết thúc nếu ta chỉ ra được :
\dfrac{(a+b+c)^2}{a^3+b^3+c^3+a+b+c-3abc}\geq \dfrac{1}{(a+b+c)}
Thế nhưng đây đơn giản chỉ là một đẳng thức, thật vậy :
\dfrac{(a+b+c)^2}{a^3+b^3+c^3+a+b+c-3abc}= \dfrac{1}{(a+b+c)}\Leftrightarrow (a+b+c)^3=a^3+b^3+c^3-3abc+a+b+c\Leftrightarrow 3(a+b)(b+c)(c+a)=-3abc+a+b+c\Leftrightarrow 3(a+b+c)(ab+bc+ca)-3abc=-3abc+a+b+c\Leftrightarrow 3(ab+bc+ca)=1
Đây chính là giả thiết bài toán. Tóm lại ta có điều phải chứng minh.
Người đăng: vào lúc
Nhãn:Toán Học

Không có nhận xét nào:

Đăng nhận xét

Đăng ký: Đăng Nhận xét (Atom)